시계열 분석(Time Series Analysis)
일정한 시간 간경으로 기록된 자료들에 대하여 특성을 파악하고 미래를 예측하는 분석 방법
가까운 미래에 있을 날씨 예측, 주식 예측, 판매 예측 등의 목적으로 사용된다.
시계열 분석에서는 ‘자기 상관 계수’ 개념이 중요하다.
정상성 시계열 & 비정상성 시계열
정상성 시계열 데이터는 평균이 일정하고, 분산이 시점에 의존하지 않는 등의 일정한 조건을 요구한다.
대부분의 자료가 비정상성이기 때문에 시계열 분석을 위해서 정상성 시계열로 변환하여야 한다.
정상성 조건
1. 일정한 평균
모든 시점에 대하여 평균이 일정해야 한다. (일정하지 않을 경우 차분을 통해서 정상화)
> rate<-c(1072, 1081, 1090, 1065, 1087, 1085, 1130, 1130, 1122, 1122, 1144, 1121, 1131, 1129, 1137, 1146, 1176, 1194, 1174, 1200, 1224, 1213, 1172, 1197)
> plot(rate, type='l')
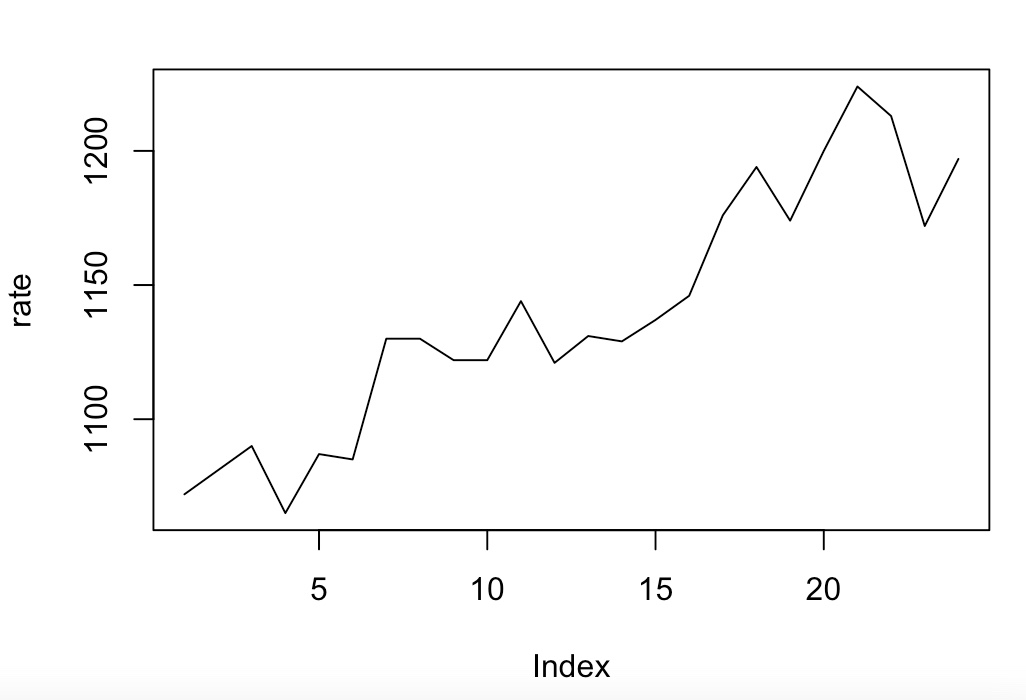
위 데이터는 평균이 일정하지 않다.(정상성이 위배된다.)
#1회 차분
> rate_diff<-diff(rate, lag=1)
> plot(rate_diff, type='l')
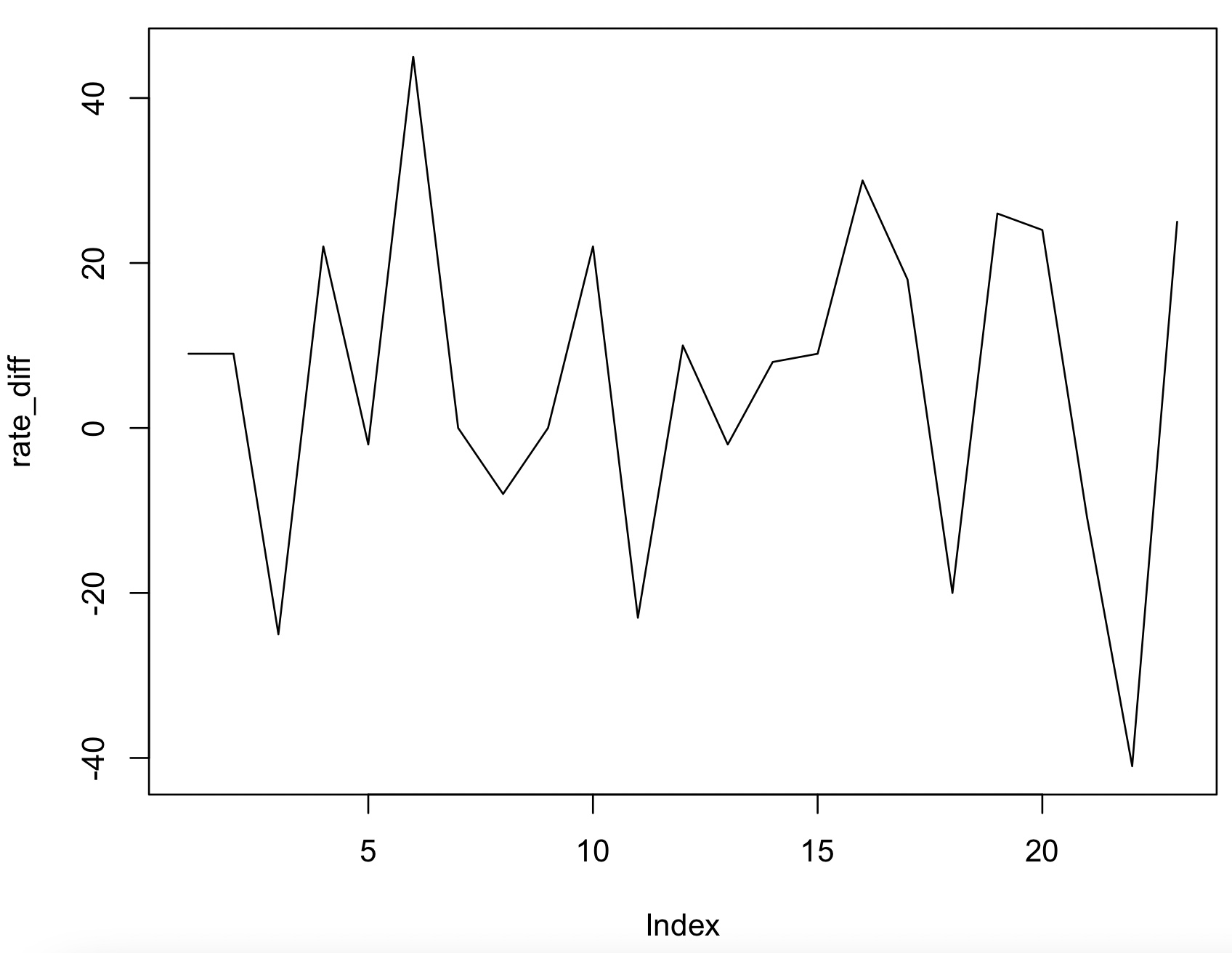
2. 일정한 분산
모든 시점에 대하여 분산이 일정해야 한다.
자료 값에 지수 혹은 로그를 취해 변환하여 시간에 따라서 변하는 분산의 크기를 안정화 시킨다.
# R 내장 시계열 데이터 UKgas
> plot(UKgas)

시간에 흐름에 따라 분산이 일정하지 않다고 판단되어 정상성에 위배
#자연 상수 e를 밑으로 하는 log를 취하여 변환을 실시
> UKgas_log<-log(UKgas)
> plot(UKgas_log)

3. 시차에만 의존하는 공분산
공분산은 시차에만 의존하고, 특정한 시점에 의존하지 않는다.
# 시차 3을 가지는 시계열 자료의 산점도
> data<-rnorm(100)
> diff<-3
> x<-1:(100-diff)
> y<-x+diff
> plot(data[x], data[y])

> cov(data[x], data[y])
[1] 0.1470773
특정 시점이 아닌 특정 시차에 영향을 받는 공분산 값